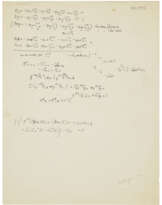Albert Einstein (1879-1955) - photo 1
Albert Einstein (1879-1955) - photo 2

Albert Einstein (1879-1955)

Lot 79
10.07.2024 10:30UTC +00:00
Classic
Starting price
£ 40 000
AuctioneerCHRISTIE'S
Event locationUnited Kingdom, London
Buyer Premiumsee on Website%
Archive
The auction is completed. No bids can be placed anymore.
Archive
ID 1249825
Lot 79 | Albert Einstein (1879-1955)
Estimate value
£ 40 000 – 60 000
Albert Einstein (1879-1955)
Autograph letter signed (with initials, 'A.E.') to Melanie Serbu, Huntington, Long Island, 15 July 1937
In German. Two pages, 280 x 2150mm, ten mathematical formulae (including Newton’s second law of motion) within the text.

'On the concept of liquids as quasi-solids': Einstein mentoring a young female scientist, renewing themes from his own doctoral thesis of 1905. Einstein recommends a course of research for Serbu’s doctoral dissertation, on testing viscosity theory by modelling the deformation of liquids, and sketches out the mathematical formulas for a theoretical treatment.

'I am glad that you agree with me on the concept of liquids as quasi-solids. Do not talk too much about this matter with others; I actually think that this could later make a nice topic for your doctoral thesis, and I am thinking primarily of the theoretical implementation of the idea. It probably won't be entirely new. For example, in gas theory the term "relaxation time" (Boltzmann) is common and has something to do with this. / I will outline the matter for you as regards pure shear deformations ...'. Einstein goes on to express the question in scientific terms, defining terms for shear force and elongation, and setting out an equation for their relationship in an ideal solid body, and thence in a fluid, introducing terms for increasing deformation or relaxation to produce a first equation, and then providing a second 'equation of motion (mass.acceleration= force)': the two equations together 'determine the movement ... But what about viscosity?'. Einstein then derives a viscosity coefficient from equation I, and shows how the relaxation rate can be derived from this: 'You can now amuse yourself by integrating Equations I and II for temporal sinusoidal waves. One can thus predict how high the frequencies need to be in order for the behaviour of the liquid in relation to waves to be noticeably different from the predictions of the usual viscosity theory. According to this, the left side in [equation] I may be neglected in comparison with the second term on the right side'; he suggests an equation which can replace equation l, and concludes 'One has in fact all the transitions between a solid body and an ideal viscous fluid'.

The present letter's theme of testing viscosity theory is immediately reminiscent of Einstein’s doctoral thesis, 'A New Determination of Molecular Dimensions' (1905), a work which had incalculable implications for the development of 20th century science both practically and methodologically, and remains Einstein’s most cited work. By working statistically with the viscosity factors of liquids, Einstein's thesis derives a new theoretical method for calculating the size of atoms and molecules. Einstein himself immediately applied his findings and methodology to the problem of Brownian motion, thereby proving both the actual physical existence of atoms and the validity of the molecular-kinetic theory of thermodynamics. Einstein was in fact a pioneer in the field of statistical mechanics, developing his own distinctively elegant and 'economical' methodology in the 1902-04 period and immediately applying it to real physical problems in 1905 (including his Nobel- Prize winning work with the photon). When Jean Perrin empirically confirmed the existence of atoms in 1908 (for which he won the Nobel Prize in 1926), Einstein’s statistical approach to problem-solving became the methodological paradigm for 20th century physics (including probabilistic quantum mechanics).

Here, 32 years later, he returns to the question of viscosity, prompted by his correspondence with the young Romanian mathematician Melanie Serbu (1909-1979): in May 1937, she had quizzed Einstein on her view of the differing states of matter (solid, liquid, gas), and the potential for viewing them as on a continuum of differing degrees of viscosity. In a letter of 25 May 1937, Einstein initially disagreed with her characterisation of solid bodies, but put forward his own view that liquids may be considered as solid bodies with low resistance to deformation. The present letter goes a step further in testing the prevailing theory of viscosity by examining 'all the transitions between a solid body and an ideal viscous fluid'. Serbu did in fact go on to work on viscosity in her dissertation, although not on the lines sketched by Einstein here. Her correspondence with Einstein had begun as early as 1928, when she was only 19; in the post-war years she went on to work as a mathematician at the university of Braşov, before emigrating to Israel in 1958.

Given Einstein’s own desire for secrecy in the matter of this letter, one can only speculate what physical application Einstein might have had in mind with the theoretical analysis he is here proposing. Einstein did considerable work with molecular physics over course of his career – ranging from Bose-Einstein condensates to mass-energy ratios in ideal gas – and it is entirely possible that he is here contemplating further work with quantum-mechanical phases of matter. This letter has not been formally published, and it appears to be unstudied by historians of science.
Address of auction CHRISTIE'S
8 King Street, St. James's
SW1Y 6QT London
United Kingdom
Preview
10.07.2024 – 10.07.2024
Phone +44 (0)20 7839 9060
Email
4FQ.AYGKAGLUQ@FO3G@
Buyer Premium see on Website
Conditions of purchaseConditions of purchase

More from Creator

A signed photograph
A signed photograph
$100
"Demostracion de la no existencia de campos gravitacionales sin singularidades de masa total no nula"
$5 500
An endorsed check to the United Jewish Appeal
An endorsed check to the United Jewish Appeal
$100
Albert Einstein (1879-1955)
Albert Einstein (1879-1955)
£18 000
Albert Einstein (1879-1955)
Albert Einstein (1879-1955)
£8 000
Albert Einstein (1879-1955)
Albert Einstein (1879-1955)
£7 000
EINSTEIN, Albert (1879-1955)
EINSTEIN, Albert (1879-1955)
£70 000
EINSTEIN, Albert (1879-1955)
EINSTEIN, Albert (1879-1955)
£10 000

Related terms

Frequently asked questions

First of all, you should register to be able to purchase at auction. After confirming your email address, enter your personal information in your user profile, such as your first name, last name, and mail address. Choose a lot from the upcoming auction and the maximum amount you want to place on it. After confirmation of your choice, we will send your application by e-mail to the appropriate auction house. If the auction house accepts a request, it will participate in the auction. You can view the current status of a bid at any time in your personal account in the "Bids" section.
Auctions are performed by auction houses and each of the auction houses describes their terms of auction. You can see the texts in the section "Auction information".
The results of the auction are published within a few days after the end of the auction. In the top menu of the site, find the tab "Auctions". Click on it and you will be on the auction catalog page, where you can easily find the category "Results". After opening it, select the desired auction from the list, enter and view the current status of the interested lot.
The information about the auction winners is confidential. The auction winner will receive a direct notification from the auction house responsible with instructions for further action: an invoice for payment and the manner in which the goods will be received.
Each of the auction houses has its own payment policy for the won lots. All auction houses accept bank transfers, most of them accept credit card payments. In the near future you will find detailed information for each case in the section "Auction information" on the page of the auction catalog and the lot.
Shipment of the won lot depends on its size. Small items can be delivered by post. Larger lots are sent by courier. Employees of the auction houses will offer you a wide range to choose from.
No. The archive serves as a reference for the study of auction prices, photographs and descriptions of works of art.