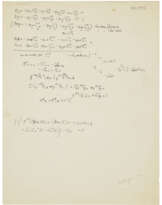EINSTEIN, Albert (1879-1955) - фото 1
EINSTEIN, Albert (1879-1955) - фото 2

EINSTEIN, Albert (1879-1955)

Лот 75
13.07.2022 10:30UTC +00:00
Classic
Продан
£ 22 680
AuctioneerCHRISTIE'S
Место проведенияВеликобритания, London
Комиссияsee on Website%
Архив
Аукцион завершен. Ставки на лот больше не принимаются.
Archive
ID 794421
Лот 75 | EINSTEIN, Albert (1879-1955)
Оценочная стоимость
£ 18 000 – 25 000
EINSTEIN, Albert (1879-1955)

Autograph letter signed ('A. Einstein') to Ernst Gabor Straus, Princeton, 26 February [1950].

In German. Two pages, 279 x 216mm, including 9 scientific formulas, and numerous other scientific terms within the text.



On symmetry transformations in one of his last models for unified field theory. 'The information about your work is truly surprising for a non-expert like me. It feels like a sort of miracle that the existence of integer-valued derivatives has some connection with the existence of linear differential equations with constant coefficients'. The body of the letter is a dense scientific discussion, in which Einstein argues at length for his preference for a form of a symmetry transformation ('Λ-transformation') based on a real rather than complex term Γ (part of the coordinates for the displacement field), discusses a demonstration he has given in the 'addendum to the appendix' showing the mathematical equivalence between two equation systems, and analyses the utility of his '"special" Λ-transformation' with the aid of a series of formulas, including numbered references to equations (presumably in their joint paper).



The utility of the "special" Λ-transformation is based on two circumstances.

1) It makes it possible, by subsequent determination of Λi (normalisation), to make the Γi equal to 0.

2) The transformation (2) is such that the addition Rik on the right side depends on the Λi alone, but not on the Γ (whereby Rikx depends on the Γx exactly as Rik depends on the Γ). This is based on the fact that

∫gikRikx dτ

turns into ∫gik[Rik - (Λi,k - Λk,i)]dτ

whereby Γ enters into the latter variational principle in exactly the same way as Γx enters into the first variational principle. Therefore, the variation of the second variational principle according to the Γ also yields the equation (3), which after normalisation of the Λi certainly passes into the equation

gik , s = 0 ... (4)

with the condition Γi = 0.



He concludes by pointing to a flaw in Straus's proposed approach: 'In the Λ-µ transformation you propose, the addition to Rik in the second form of the variational principle would explicitly depend on the Γ, so the variation after the Γ does not lead to (4), and not at all to a transmutation-invariant equation in general. / Therefore, despite great freedom in regard to normalisation, there would be no advantage for the formulation of the field equations'. A postscript refers to his repeated attacks on the McCarthyite 'wi[t]ch hunt' (he gives the term in English).



The German-American mathematician Ernst Gabor Straus (1922-1983) was Einstein's assistant at Princeton for four years between 1944 and 1948, during which period they produced three joint papers. The discussion in the letter is closely related to the proposed basis for a unified field theory published in the last of these, 'A Generalization of the Relativistic Theory of Gravitation, II' (Annals of Mathematics, Second Series, Vol. 47, No. 4 (Oct., 1946), pp. 731-741). Einstein had summarised the approach in Appendix II of the third edition of The Meaning of Relativity (1950), to which he refers in ths letter.





Special notice


This lot has been imported from outside of the UK for sale and placed under the Temporary Admission regime. Import VAT is payable at 5% on the hammer price. VAT at 20% will be added to the buyer’s premium but will not be shown separately on our invoice.
Адрес торгов CHRISTIE'S
8 King Street, St. James's
SW1Y 6QT London
Великобритания
Предосмотр
13.07.2022 – 13.07.2022
Телефон +44 (0)20 7839 9060
E-mail
4FQ.AYGKAGLUQ@FO3G@
Комиссия see on Website
Условия использованияУсловия использования

Больше от Создателя

A signed photograph
A signed photograph
$100
"Demostracion de la no existencia de campos gravitacionales sin singularidades de masa total no nula"
$5 500
An endorsed check to the United Jewish Appeal
An endorsed check to the United Jewish Appeal
$100
Albert Einstein (1879-1955)
Albert Einstein (1879-1955)
£18 000
Albert Einstein (1879-1955)
Albert Einstein (1879-1955)
£8 000
Albert Einstein (1879-1955)
Albert Einstein (1879-1955)
£7 000
Albert Einstein (1879-1955)
Albert Einstein (1879-1955)
£40 000
On his family's applications for U.S. citizenship
On his family's applications for U.S. citizenship
$100

Связанные термины

Часто задаваемые вопросы

  1. Зарегистрируйтесь на сайте как «Покупатель», чтобы учавствовать на аукционах. Регистрация бесплатна. Подтвердите email и после этого вы получаете доступ в личный кабинет.
  2. Выберите лот, который вы хотите купить, нажмите на кнопку «Сделать ставку». В открывшемся окне выберете сумму для ставки и подтвердите ее.
  3. Мы направим оповещение о ставке в аукционный дом и сообщим вам по эл. почте, когда аукционный дом ее подтвердит. Статус ставки вы можете видеть и в вашем личном кабинете во вкладке «Ставки».
Торги проводят аукционные дома и каждый из аукционных домов описывает собственные условия проведения торгов. Тексты вы можете увидеть на странице лота, кликнув на ссылку «Условия использования» в разделе «Информация о торгах»
Результаты аукциона публикуются в течении нескольких дней после завершения аукциона. В верхнем меню сайта найдите закладку «Аукционы». Нажав на нее, вы попадете на страницу аукционных каталогов, где без труда отыщете рубрику «Результаты». Открыв ее, выберите из списка нужный аукцион, войдите и просмотрите текущее состояние интересующего лота.
Данные о победителях аукционов конфиденциальны. Победитель аукциона получает оповещение напрямую из ответственного аукционного дома с инструкцией к дальнейшим действиям: счет на оплату и способы получения выигрыша.
Каждый из аукционных домов имеет собственную политику оплат выигранных лотов. Все аукционные дома принимают банковские переводы, большинство из них принимают оплату кредитными картами. В ближайшее время Вы найдете для каждого конкретного случая подробную информацию в рубрике «Информация о торгах» на станице аукционного каталога и лота.
Пересылка выигранного лота зависит от его размера. Мелкие предметы могут быть доставлены почтовой пересылкой. Более крупные лоты направляются курьерской службой. Служащие аукционных домов предложат Вам различные возможности на выбор.
Нет. Архив служит справочником для изучения аукционных цен, фотографий и описаний произведений искусства.
?>